Wstęp
Rozwój metod klasyfikacyjnych, skutkuje zastąpieniem popularnych dotychczas metod przez nowsze i wydajniejsze algorytmy np. popularny model Random Forest zostaje zastąpiony przez sieci neuronowe. Pomimo tego, że te metody dają mnóstwo nowych możliwości, wyznaczają również szereg nowych wyzwań dla technologów. Sieci neuronowe posiadają charakter modeli czarnoskrzynkowych - czyli takich, których reguły klasyfikacji nie są znane użytkownikowi. W rezultacie obszary wystąpienia błędów nie są możliwe do przewidzenia. Pomimo iż modele klasyfikujące chmurę punktów są w obecnym momencie bardzo wydajne, wciąż istnieje potrzeba wprowadzania poprawek. Stworzenie narzędzia do poprawy klasyfikacji wymaga implementacji miarodajnego narzędzia do ewaluacji stopnia poprawy. Algorytm oczyszczający oprócz poprawy ma na celu zmniejszenie liczby czynności przy wykonywaniu ręcznej poprawy oraz redystrybucję punktów w klasie ułatwiając manualną edycję.
Zarówno w przypadku wprowadzania poprawek ręcznych jak i tych automatycznych istnieje potrzeba ewaluacji stopnia poprawy. Powszechnie stosowane metryki ewaluacji, takie jak Dokładność, czy F1 nie są w tym przypadku miarodajne. W przypadku chmury punktów w rozmiarze 5e+6 punktów, przy założeniu wstępnym, że 3e+4 to próbki błędnie sklasyfikowane, dokładność jest na poziomie 0.994. Po skutecznym poprawieniu błędu (do 15e+3) dokładność zwiększyła się do 0.997. O ile dokładność zmieniła się nieznacznie, zmiana w liczbie oczyszczonych próbek zmieniła się o ponad połowę. Ponadto nie posiadamy żadnych dodatkowych informacji dotyczących typów błędów.

W ramach rozwoju metod związanych z testowaniem analizowaliśmy typy błędów jakie występują w klasyfikacji oraz przy poprawie jakości klasyfikacji. Stworzyliśmy podejście w którym przeanalizowaliśmy zmianę przynależności na poziomie segmentu-grup bliskich punktów. W rezultacie wyznaczyliśmy 5 typów błędów.
Algorytm
W pierwszym kroku wyznaczyliśmy błędy klasyfikacji referencyjnej, predykcji oraz predykcji poddanej poprawce automatycznej. Do wyznaczenia klastrów użyliśmy algorytmu bazującego na zmienności w gęstości przestrzennej punktów - DBSCAN.
Neps (p) = {q ∈ D : d(p,q) < ε }
ε -obszar wyszukiwania sąsiedniego punktu,
p - punkt rdzeniowy,
q - punkt w epsilonowej () odległości względem punktu rdzeniowego.
DBSCAN przypisuje odrębne segmenty dla punktów znajdujących się w większej odległości niż wartość, co pozwala wyznaczyć skoncentrowane grupy punktów z pominięciem punktów odstających. Następnie porównaliśmy błędy przed i po poprawieniu klasyfikacji. W ten sposób uzyskaliśmy segmenty wszystkich błędnych próbek, z możliwością przeanalizowania błędów przed i po oczyszczeniem.
| Opis błędu | Schemat | |
| Typ 1. |
Wszystkie punkty zostały poprawione przez algorytm klasyfikujący. W rezultacie wszystkie punkty zostały |
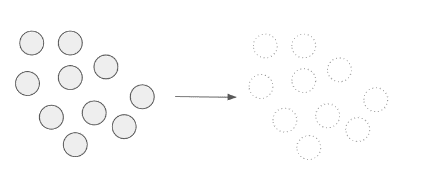 |
| Typ 2. |
Liczba punktów w segmencie błędu nie zmieniła się - oczyszczanie/poprawianie klasyfikacji nie przyniosło rezultatu. Liczba punktów w segmencie błędu nie uległa zmianie. |
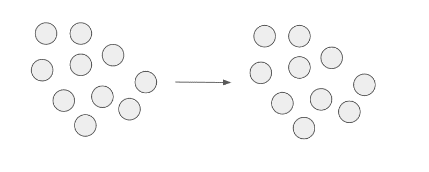 |
| Typ 3. |
Ten typ błędu opiera się na tym, że część punktów została poprawiona i tym samym usunięta z segmentu błędu. Istniejący segment zostaje pomniejszony o poprawione próbki. |
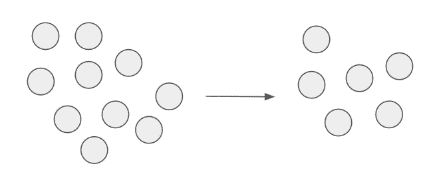 |
| Typ 4. |
Liczba punktów zmieniła się, bez korzyści poprawy - powstały nowe segmenty. Algorytm nieprawidłowo zidentyfikował punkty zaklasyfikowane poprawnie. |
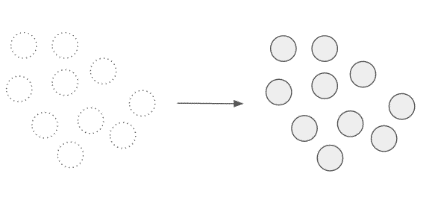 |
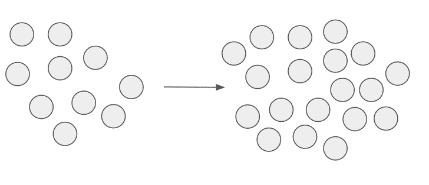
| Typ 5. |
Segment błędu jednocześnie nie został poprawiony oraz powiększony o dodatkowe punkty błędnie sklasyfikowane. Oznacza to, że algorytm poprawiający klasyfikację, nieprawidłowo przypisał klasę do tych punktów. |
 |
Wnioski
Podejście analizowania zmian w liczbie segmentów błędów ułatwia analizę wpływu poprawek klasyfikacji na ostateczny rezultat i wygląd sklasyfikowanej chmury punktów. Dostarcza informacji w jaki sposób algorytm oczyszczający zmienia postać występujących błędów.



